$\dot{x}\left(t\right)=f\left[x\left(t\right),u\left(t\right)\right]$	équation d'état
$v\left(t\right)=g\left[x\left(t\right),u\left(t\right)\right]$	équation de sortie,

et pour les systèmes linéaires

$\dot{x}\left(t\right)=A\cdot x\left(t\right)+B\cdot u\left(t\right)$	équation d'état
$v\left(t\right)=C\cdot x\left(t\right)+D\cdot u\left(t\right)$	équation de sortie,

à partir desquelles la course des éléments du vecteur de sortie v(t) peut être calculée, avec des valeurs initiales connues des éléments du vecteur x(t) à tout instant t₀ (souvent avec t₀ = 0), avec une course connue des éléments du vecteur d’entrée u(t), et en partant de t₀

VOIR: Figure 3.

Note 1 à l'article: En cas de variables à temps discret, les équations sont les suivantes:

xi+1 = f (xi, ui)	équation d'état
vi = g (xi, ui)	équation de sortie,

et pour les systèmes linéaires

xi+1 = Φ·xi + H·ui	équation d'état
vi = C·xi + D·ui	équation de sortie.

Note 2 à l'article: Cet article était numéroté 351-21-08 dans la CEI 60050-351:2006.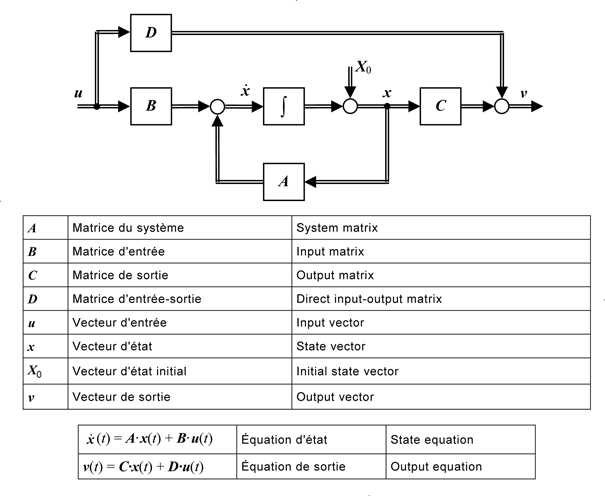

Figure 3 – Linear transfer system with state variables

Figure 3 – Système de transfert linéaire avec variables d'état