| Area |
 |
Mathematics - Functions / Distributions |
 |
|
| IEV ref |
 |
103-03-05 |
 |
|
Symbol |
 |
δ |
 |
|
en |
 |
Dirac function
Dirac delta function
unit pulse
unit impulse, US |
 |
 |
distribution assigning to any function f(x), continuous for , the value f(0) Note 1 to entry: The Dirac function can be considered as the limit of a function, equal to zero outside a small interval containing the origin, and the integral of which remains equal to unity when this interval tends to zero. See Figure 2, where instead of a triangle any other shape with area 1 is possible, too. Note 2 to entry: The Dirac function is the derivative of the unit step function considered as a distribution. Note 3 to entry: The Dirac function can be defined for any value x0 of the variable x. The usual notation is: 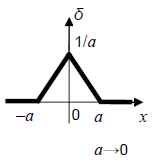
Figure 1 – Distribution de Dirac Figure 1 – Dirac function |
 |
|
fr |
 |
distribution de Dirac, f
impulsion unité, f
percussion unité, f |
 |
 |
distribution associant à toute fonction f(x), continue pour , la valeur f(0) Note 1 à l'article: La distribution de Dirac peut être considérée comme la limite d'une fonction nulle en dehors d'un petit intervalle contenant l'origine et dont l'intégrale reste égale à l'unité lorsque cet intervalle tend vers zéro. Voir la Figure 2, où le triangle peut être remplacé par n’importe quelle forme d’aire unité. Note 2 à l'article: La distribution de Dirac est la dérivée de la fonction échelon unité considérée comme une distribution. Note 3 à l'article: La distribution de Dirac peut être définie pour toute valeur x0 de la variable x. La notation usuelle est: |
 |
|
ar |
 |
دالة ديراك
دالة ديراك التركيبية
النبضة الواحدة
قفزة الوحدة |
|
cs |
 |
Diracova funkce
Diracova delta-funkce
δ-funkce
jednotkový pulz |
|
de |
 |
Dirac-Funktion, f
Delta-Distribution, f
Einheitsstoßfunktion, f |
|
es |
 |
distribución de Dirac |
|
it |
 |
distribuzione di Dirac
funzione delta di Dirac
impulso unitario |
|
ko |
 |
다이락 함수
다이락 델타 함수
단위 펄스 |
|
ja |
 |
ディラック関数
ディラックのデルタ関数
単位パルス
単位インパルス |
|
|
|
|
pl |
 |
dystrybucja Diraca
delta Diraca
impuls jednostkowy
funkcja Diraca (termin niezalecany) |
|
pt |
 |
função de Dirac
impulso unitário |
|
sr |
 |
Диракова функција, ж јд
јединична импулсна функција, ж јд |
|
sv |
 |
Diracs deltafunktion
Diracs funktion
enhetspuls |
|
zh |
 |
狄拉克函数
狄拉克δ 函数
单位脉冲函数
单位冲激函数 |